Definite description
From Wikipedia, the free encyclopedia
A
definite description is a
denoting phrase in the form of "the X" where X is a noun-phrase or a singular common
noun. The definite description is
proper if X applies to a unique individual or object. For example: "the first person in space" and "the 42nd President of the United States of America", are proper. The definite descriptions "the person in space" and "the Senator from Ohio" are
improper because the noun phrase X applies to more than one thing, and the definite descriptions "the first man on Mars" and "the Senator from Washington D.C." are
improper because X applies to nothing. Improper descriptions raise some difficult questions about the
law of excluded middle,
denotation,
modality, and mental content.
[edit] Russell's analysis
France is presently a
republic, and has no king. Consider the statement "The present King of France is bald."
Bertrand Russell wished to answer the question: Is this statement true, false, or is it meaningless?
It does not seem to be true, for there is no present King of France. But if it is false, then one would suppose that the negation of the statement, that is, "It is not the case that the present King of France is bald," or its
logical equivalent, "The present King of France is not bald," is true. But that seems no more true than the original statement.
Is it meaningless, then? One might suppose so (and some philosophers have; see below) because it certainly does fail to refer, but on the other hand it seems to mean something that we can quite clearly understand.
Russell, extending the work of
Gottlob Frege, proposed according to his
theory of descriptions that when we say "the present King of France is bald", we are implicitly making three separate existential assertions:
- there is an x such that x is a present King of France (∃x(Fx))
- for every x that is a present King of France and every y that is a present King of France, x is y (i.e., there is at most one present King of France) (∀x(Fx → ∀y(Fy → y=x)))
- for every x that is a present King of France, x is bald. (∀x(Fx → Bx))
Taken together, these say that the present King of France is bald, which is usually expressed like so (there is some x such that x is the present King of France, and if anything happens to be the present King of France, it is x, and x is bald):
-
- ∃x(Fx & ∀y(Fy → y=x) & Bx)
This is false, since there is nothing that fulfills the existential clause (that "there is some x such that...").
The negation of this definite description is ambiguous. When we say "the present King of France is not bald," do we mean that he's not bald because there is no King of France? If so we would render the sentence thus:
-
- ~∃x(Fx & ∀y(Fy → y=x) & Bx)
That is to say, there is nothing that fulfills the conditions of being the present King of France, and being the only present King of France, and being bald. This is
true.
But now suppose that when we say "the present King of France is not bald," we mean that the thing that is the present King of France isn't bald (perhaps we mistakenly believe that there is a King of France). This would be rendered like so:
-
- ∃x(Fx & ∀y(Fy → y=x) & ~Bx)
This says, there is something that is the King of France, and anything that is the present King of France is that thing, and that thing is not bald. This is false.
Thus, "the present King of France is not bald" is
both true and false, breaking the
law of the excluded middle, though not at the level of logical rendering. In neither case is it meaningless or lacking in truth value, though there be no King of France.
Russell's analysis has been attacked by
P.F. Strawson,
Keith Donnellan and others, and it has been defended and refined by
Stephen Neale.
[edit] Symbolic form
When using the definite descriptor in a
formal logic context, it can be symbolized by

, so that
- ιx(φx)
means "the

such that

", and
- ψ(ιx(φx))
is equivalent to "There is exactly one
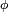
and it has the property

":

[edit] References
- Donnellan, Keith, "Reference and Definite Descriptions," in Philosophical Review 75 (1966): 281-304.
- Neale, Stephen, Descriptions, MIT Press, 1990.
- Ostertag, Gary (ed.). (1998) Definite Descriptions: A Reader Bradford, MIT Press. (Includes Donnellan (1966), Chapter 3 of Neale (1990), Russell (1905), and Strawson (1950).)
- Reimer, Marga and Bezuidenhout, Anne (eds.) (2004), Descriptions and Beyond, Clarendon Press, Oxford
- Russell, Bertrand, "On Denoting," in Mind 14 (1905): 479-493. Online text
- Strawson, P. F., "On Referring," in Mind 59 (1950): 320-344.
[edit] See also
[edit] External links
 , so that
, so that such that
such that  ", and
", and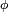 and it has the property
and it has the property  ":
":
